Math, Maxwell’s Equations, Nabla, and Statistics
Today I read works from Steven Strogatz and Daniel Fleisch. Both were on math, on fairly different topics, and hence lead to this somewhat mixed title.
A while ago I linked to Steven Strogatz’s series on mathematics in the New York times. The series seems to have come to an end, with some interesting new stories, on integration, differentiation. and probability among others. Here’s an interesting quote on his essay on change:
There’s a more general principle at work here — things always change slowest at the top or the bottom. It’s especially noticeable here in Ithaca. During the darkest depths of winter, the days are not just unmercifully short; they barely improve from one to the next. Whereas now that spring is popping, the days are lengthening rapidly. All of this makes sense. Change is most sluggish at the extremes precisely because the derivative is zero there. Things stand still, momentarily.
Recently, I have read somewhere about Daniel Fleisch and his book “A Student’s Guide to Maxwell’s Equations“. At first glance, I have nothing to do with Maxwell’s equations. However, I thought that a field is a field, be it electric potential or water pressure. First, this is the first time I read a book that was that clearly structured. Essentially each of the four laws (Gauss laws for electric and magnetic fields, Faraday’s law, and Ampere-Maxwell law) cover one chapter, and the final chapter is about how Maxwell “developed his comprehensive theory of electromagnetism” by considering these four equations in combination. This seems not like anything special. However, the structure is in each chapter essentially identical: first the terms of the mathematical equation are briefly explained, then there’s a section on what this is about, the physical meaning, and then there are sub-chapters on every term, sometimes “only” on the sign (in the case of Lenz’s law). I think the critical factor that makes this approach superior to other approaches is how Fleisch links between the equations. Where are similarities in equations? Are they because of similar physical processes? And how are physical processes covered mathematically?
Why do I think all this is relevant? In most disciplines I have worked in, this way of thinking is important: How is a process covered in mathematics. Even more, the way of thinking is essentially the same — it doesn’t matter what kind of field you’re looking at. There is even a quote attributed to Maxwell in the preface: “… analogies are useful not because the quantities are alike but because of the corresponding relationships between quantities“. And by Fleisch: “… although nothing is actually flowing in a static electric field, you’re likely to find the analogy between a faucet (a source of fluid flow) very helpful in understanding the nature of the electrostatic field“. And I think the reverse holds true too. Additionally, Fleisch does a really excellent job in explaining details of the Nabla operator, divergence, curl, and gradient.
Here is one example taken from Fleisch’s book, which is directly relevant to statistics:
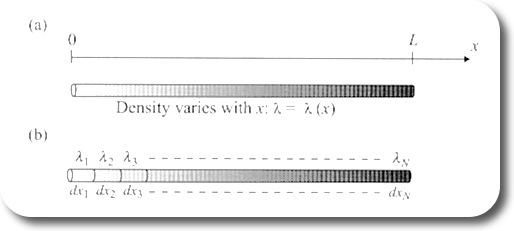
Figure 1: Line integral for a scalar function
Figure 1a (Figure 3.2 in Fleisch’s book) shows a wire with variable density. Here is how Fleisch describes what has to be done to determine the mass of the wire. In other words, what has to be done to find the distribution function from its density function.
To determine the total mass of the wire, imagine dividing the wire into a serios of short segments over each of which the linear density is approximately constant, as shown in Figure 1b. The mass of each segment is the product of the linear density of that segment times the segment length dx, and the mass of the entire wire is the sum of the segment masses
Well, it’s an integral. Nothing really fancy about that.
And regarding electromagnetics and fluid flow: Isn’t Darcy’s law nothing else than Ohm’s law? Maybe, we should brush up our complex maths 🙂
Thomas
7 Sep 10 at 11:34 am
Yes. It’s an integral. And for some of us, there’s nothing fancy about an integral anymore, because we use it on a daily basis. For others, it might be fancy. However the circumstances might be, I think it is still a very good explanation of what an integral is.
And yes, Darcy’s law and Ohm’s law and probably a few others are quite similar in their form. I think more beautiful are the similarities between properties of pressure fields in the case of fluid dynamics and the properties of electro-magnetic fields in the case of electro-dynamics (or whatever that is called then).
Claus
9 Sep 10 at 1:48 pm