Archive for 2010
Identi.ca Weekly Updates for 2010-11-17
- @seismotom I'd be happy to talk #Python How much feedback have you gotten so far? in reply to seismotom #
Identi.ca Weekly Updates for 2010-11-03
- "Running the Numbers" exhibit http://ke-we.net/6rv in Berkeley is great visualization of stats/data by http://ke-we.net/6rw (via @cbdawson) #
- TAZ titles today on #water #privatization in #Berlin http://ke-we.net/6m7 and puts the contracts online: http://ke-we.net/6m8 #
- Stories and #Statistics http://ke-we.net/6lc #
- three gorges #dam almost full for first time: http://ke-we.net/6gx #
TAZ makes Berlin Water Contracts Publicly Available
The city of Berlin has some of the highest prices for drinking water in Germany. In the last decade, water prices in Berlin have risen twice as much compared to the German average. People who felt they paid too much suspected that the high prices were related to the fact that Berlin’s drinking water infrastructure was privatized in the late 1990’s. Since then, the two involved companies RWE and Veolia made 1.3 Billion Euros profit!
Part of the problem was that the content of some of the contracts between the city who has a monopoly on supplying drinking water and RWE / Veolia, were not known to anyone other to the two parties. Some groups, like the “Berliner Wassertisch” have been campaigning to make those contracts publicly available. Planetwater.org mentioned in January 2008 Berlin’s water problem. This saturday, the Berlin-based newspaper, “die TAZ”, made those contracts public. Most notably, these contracts contained information on how the two parties had made sure that there could be profits — despite the fact that an open contract allowing profits had earlier been judged to be illegal.
A. Loiser points out in his article: “the Berlin example shows how companies are allowed to make huge, almost deliberately high, profits to the detriment of the citizens” (TAZ, 30./31. Oktober 2010, pages 16-17). It’s not the case that there was not enough water available, nor that the available water was excessively contaminated — both scenarios would lead to increased costs. Neither was the water distribution excessively difficult and expensive.
Research by Sebastian Heiser shows (article, xls sheet), how not only the profit rose, but costs for employees as well as costs for investments diminished between 1999 and 2009.
Most politicians involved with Stuttgart 21 now agree that the public has not been included sufficiently in the decision process for the project. Hence, the arbitration led by Heiner Geisler is broadcast publicly via internet and on TV. It remains to be seen if this leads to more data being publicly available.
Recent Readings
Here are some links I recently came across, which might be relevant to the grand theme of this blog: 🙂
- The AGU has started to host an “uber-blog“: it includes seven blogs by independent geo-scientists and three blogs by AGU staff on AGU meetings, on science communication, and general AGU sciences;
- Daniel Stellar at the Columbia Water Center wrote on the relationship between water quantity and quality;
The journal “Foreign Policy” published an article on the role of China, other Asian states, and the USA in the Mekong River basin;
[foreign secretary] Clinton recently met with the foreign ministers of Cambodia, Laos, Thailand, and Vietnam and pledged $187 million to support the Lower Mekong Initiative, which has the stated aim of improving education, health, infrastructure, and the environment in the region.
- Anne Jefferson, wrote on “Highly Allochthonous” how she uses rock samples to teach students on porosity and effective parameters;
- The Telegraph reports that “Scientists create dry water” — and see use of it to increase safety of potentially harmful liquids during transport;
- Peter Gleick: “The Human Right to Water, at Last“;
- Finally, the Scientific Fundamentalist write about “]Why Intelligent People Drink More Alcohol][9]”;
R.I.P. Benoît Mandelbrot
Here are his orbituaries at Wired and at the NY Times.
update Saturday; October 23, 2010:
More on Mandelbrot’s work and “his set” at the Wolfram Blog
Identi.ca Weekly Updates for 2010-10-20
- nice example of #calculating #probabilities based on possibilities: summer births ? more boy births? http://ke-we.net/5tf #
- "when construction costs runneth over": irrational optimism planning major building projects #rail #tunnel NJ-NY #s21 http://ke-we.net/5tb #
Identi.ca Weekly Updates for 2010-10-13
- Blog Action Day 2010 on Friday, Oct. 15th!: #clean #water to drink for everyone! #BAD2010 @blogactionday #
October 15th – Blog Action Day
This is a quick notice, that this coming friday, October 15th, is Blog Action Day!
Each year bloggers from more than 100 countries come together and blog about a single important issue, and this year’s topic is clean water. There is a petition to the UN on supplying clean drinking water to everybody.
For more, please check back on October 15th!
Random Numbers
The importance of random numbers is often overlooked. Even the people who should realize their importance take their existence for granted. Uniform random numbers are a function and then they are generated. Ok, the ones in Excel are not the greatest. The typical ones in programming languages are ok. Some people have their special random numbers.
There are a few interesting ways to generate random numbers: My favourite to date was the lava lamp random generator, whose current version can be found online here and doesn’t require an actual lava lamp anymore.

A lava lamp could be the source for random numbers
I just found out about a novel approach. Christian Gabriel at the Institute for Optics, Information and Photonics at the University of Erlangen, Germany recently published a novel method to generate random numbers: He proposed to
use vacuum fluctuations as quantum dice. Such fluctuations are another characteristic of the quantum world: there is nothing that does not exist there. Even in absolute darkness, the energy of a half photon is available and, although it remains invisible, it leaves tracks that are detectable in sophisticated measurements: these tracks take the form of quantum noise. This completely random noise only arises when the physicists look for it, that is, when they carry out a measurement. [from here]
The institute’s webpage states only that
By appropriately post-processing the measured data, truly random numbers which are solely based on quantum noise can be extracted.
I guess I would have to read the paper in detail what role the gaussian distribution plays and how the post-processing works exactly. In any way, this sure sounds like an interesting approach!
Bivariate Statistical Functions, Conditional Distributions
This post shows an example of a bivariate density function and its related distribution functions, conditional distribution- and conditional density functions. The examples are taken from here, plots are added. Hopefully, this post will shed some light onto the properties and characteristics of bivariate conditional functions, both density and distribution functions.
Density Function
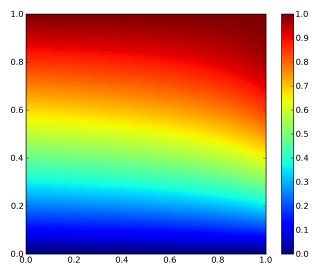
A bivariate density function is given as
$$ f_{X,Y}(x,y) = \begin{cases} 2-x-y & 0 The plot of the bivariate density is shown on Figure 1. Figure 1: Bivariate density function By integrating twice (for each variable), the bivariate distribution function is obtained: $$ F_{X,Y}(x,y) = 2xy – \frac{1}{2}x^{2}y – \frac{1}{2}xy^{2} $$ The plot of the bivariate distribution function is shown on Figure 2. Figure 2: Bivariate distribution function The conditional density function is given generally by $$ f_{X|Y}(x|y) = \frac{f_{X,Y}(x,y)}{f_{Y}(y)} $$ and $$ f_{Y|X}(y|x) = \frac{f_{X,Y}(x,y)}{f_{X}(x)} $$. The marginal distributions of X and Y are given as $$ f_{X}(x) = \sum_{y \in D(Y)} f_{X,Y}(x,y) $$ and $$ f_{Y}(y) = \sum_{x \in D(X)} f_{X,Y}(x,y) $$ For the given density function, $$ f_{Y|X}(y|x) = \frac{2-x-y}{3/2-x} $$. The contour plot of this equation is shown on Figure 3. Note that this is not identical to the conditional on y! If x is really small and just bigger than 0 then there are medium range probabilities for y to be anything between 0 and 1. If x is really big and close to 1, then the probability is much higher that y is small than that y is big. Figure 3: Conditional density of y on x. The conditional distribution function for our example for $$ 0 $$ F_{Y|X}(y|x)=\frac{(2-x)y – 1/2y^{2}}{3/2-x} $$ the contour plot of which is shown on Figure 4. The conditional distribution function is the bivariate density function integrated along one direction, devided by the marginal density of the variable that it is conditioned on (not the one along which the bivariate density is integrated along). At first glance this seems odd, cause there is a density function (the marginal density) in the expression for a distribution function. But this density is independent of the variable along which is integrated! Figure 4: Conditional distribution function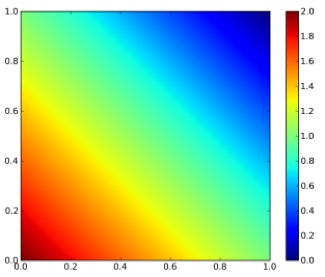
Distribution Function
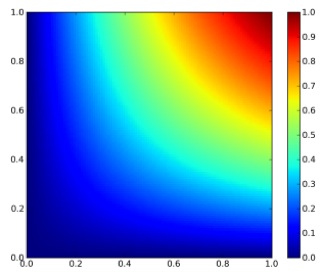
Conditional Density Function
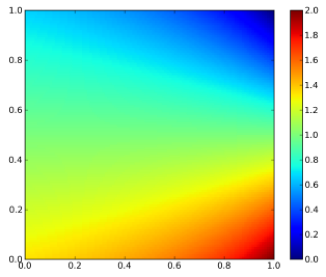
Conditional Distribution Function